Wisdom of the crowd?
November 15, 2012
Alinea, the Chicago restaurant known for combining food, science and art, recently asked people on their Facebook page to guess how many last names have made reservations at the restaurant since it opened on May 4, 2005. I decided to take stab at the question. Nerd that I am, though, I also looked at other people’s guesses - which turned out to be more interesting than answering the question itself.
Our guess
First, I estimated the total number of tables seated at Alinea since opening day. If Alinea has 20 tables (number of tables), and about 2 parties get seated at each table a night, and the restaurant is open 250 nights a year, and it’s been open for 7.5 years, that works out to 75,000 table seatings. You can only get a table at Alinea if you get a reservation and presumably they add your name to their “dining notes” database when you reserve a table. That means each of those 75,000 tables has a surname associated with it.
Second, I estimated how many of these were unique surnames -- there’s going to be a bunch of Smiths in that 75,000. Some googling turned up a list of surnames from the 2000 U.S. Census. Booyah! To get the estimate, I repeatedly took uniform-random samples of 75,000 surnames from this list, and counted the number of unique names in the samples. (Here’s the quickie python script I used to do that.)
The analysis came up with roughly 24,000 unique surnames. Also, in case people guessed the same number, Alinea proposed a tiebreaker: the number of last names that start with the letter Z. For the number of z-surnames, the analysis came up with roughly 200. To make a final guess, I picked some numbers around there that felt lucky: 24,199 unique surnames and 223 z-surnames.
There are definitely some oversimplifications with this analysis: (i) Alinea’s diners are almost certainly not a random subpopulation of the US, (ii) the U.S. population probably doesn’t represent the international range of diners that Alinea draws, and (iii) there will be repeat diners. That said, this approach is good enough for a rough estimate.
The result
About 1,200 people submitted guesses. Nick Kokonas, co-owned of Alinea, posted the answer: they’ve seated 23,980 unique surnames, and 240 z-surnames. Our guesses were good enough for the top ten (24,199 and 223), but others’ were closer - three people guessed 24,000. Two of them even had the same tiebreaker of 200!
Other people’s guesses: Wisdom of the Crowd?
As fun as that was, it was even more fun to look at other people’s guesses. Looking at the data*, they seem to be all over the place! It got me thinking as to whether this would be a good example of the Wisdom of the Crowd (if that is such a thing). The idea is that crowd averages are superior to individual judgements because the mistakes that individuals make tend to cancel out on average. So - did the mean of the crowd’s guesses turn out to be the best guess of the true number? Here’s what the distribution of guesses looks like:
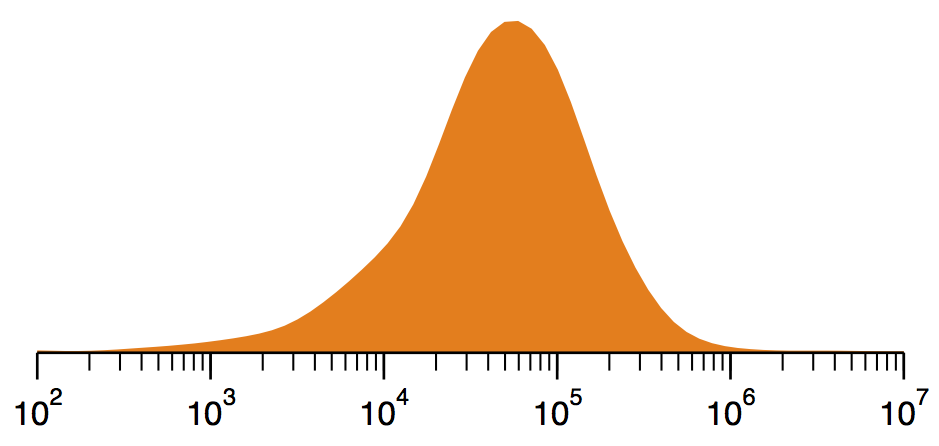
It looks like the well-known bell curve. But notice that the X axis is on a logarithmic scale. So it’s the logarithm of the guesses that roughly follows a bell curve (in other words, this is a lognormal distribution, maybe slightly skewed). What does this mean?
One way to think of it is that people’s guesses of the order of magnitude are pretty consistent, and follow a normal distribution, but their guesses of the actual value are all over the place. Because of this, the mean of people’s guesses - 98,335 - is not a good guess of the final answer at all.
Interestingly, the median - 48,754 - is closer but still pretty far off. Perhaps a reason why is that one of the key assumptions of the Wisdom of the Crowd is that people’s guesses do not influence other’s guesses. This sounds like a pretty shitty assumption in Facebook comments, eh? And it is! Here is a graph of peoples guesses over time:
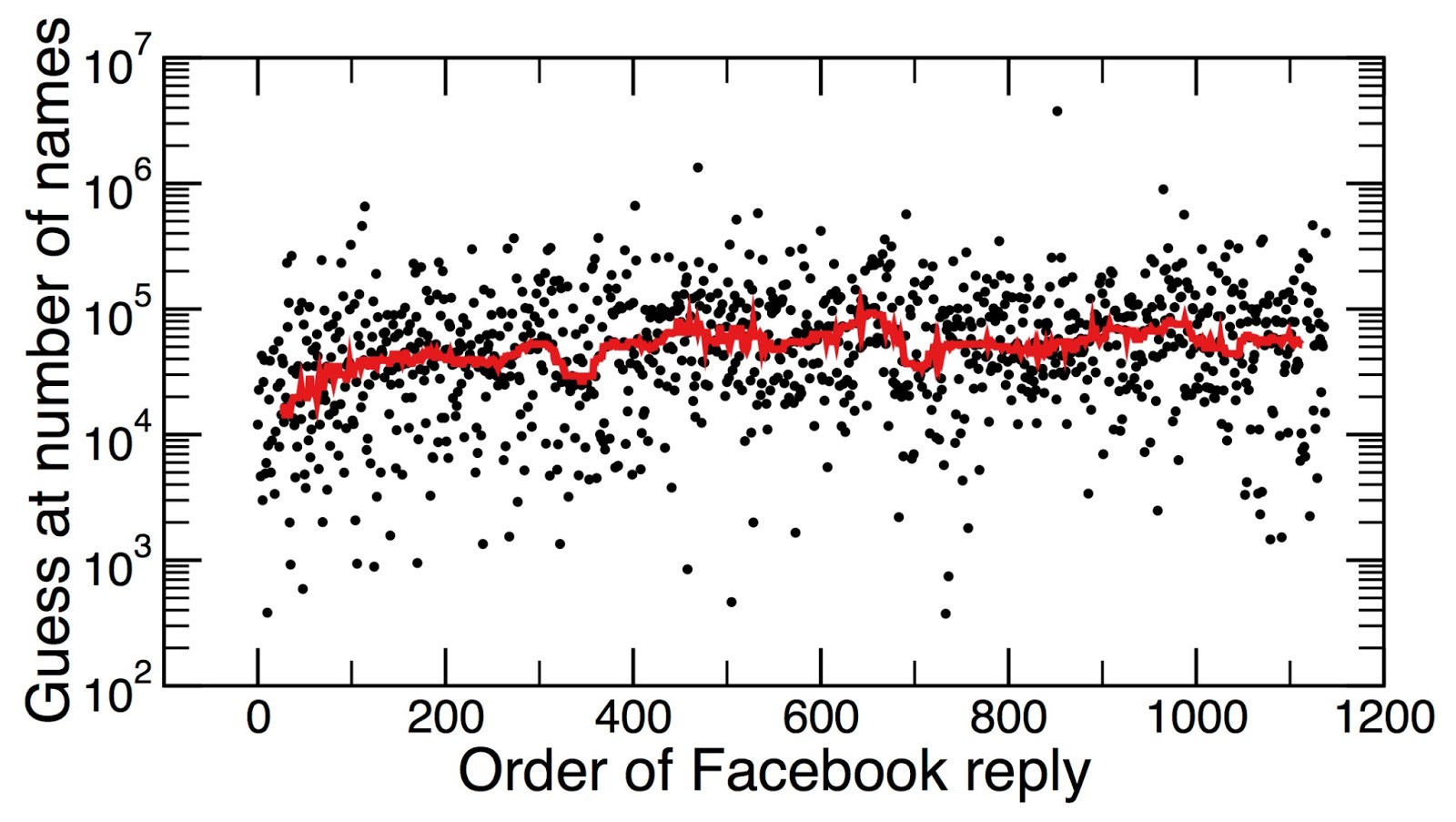
The graph is showing all the guesses on Alinea’s facebook thread up to 9pm on Wednesday night. (Keep in mind the log scale on the y axis.) The median guess increased over time - the mean of the last 50 guesses (50,136) is over three times higher than that of the first 50 guesses (15,421).
Also, there’s a lot of correlation between a person’s guess and what others guessed in the comments right before them (on Facebook, you can click to see the 50 previous comments before yours). Unsurprisingly, people are probably Price-Is-Righting and trying to find a chunk of prime guessing real-estate that the others immediately before them haven’t taken.
We love feedback
Feel free to use the comments to explain how you made your guess, or suggest improvements. Also, Grant and Nick, if you ever need some data analysis, shoot us an e-mail. :) We might work for food.
*To get at this data, I wrote another little python script to pull the numbers out of the HTML from the facebook page. For people that posted twice or more, I used their first guess. In non-guess comments, guesses of 1 and 1 were used for the total number of names and the number that start with the letter Z. Here is a CSV file with the data so that you can play around with it if you want.