Using data to dominate the NCAA tourney
March 24, 2014
I love March Madness. So much great basketball condensed in such a short time period satisfies my well-diagnosed sports illness. Incidentally, with everyone filling out brackets, March Madness also satiates my less well-diagnosed gambling urges. When one of my friends sent me an invitation to join a new type of game for March Madness, I was… intrigued.
Instead of picking teams and filling out a bracket, you instead pick players in a more fantasy based contest. The rules are fairly simple, you pick any 10 players that you think will score the most points throughout the tournament, no drafting. The participant who has the highest point total at the end of the tournament is declared the winner. There is a slight twist, based on your seed, you can multiply the points a player scores in each game as follows:
- seeds 1 - 4. Multiply points by 1
- seeds 5 - 8. Multiply points by 2
- seeds 9 - 12. Multiply points by 3
- seeds 13 - 16. Multiply points by 4
Sounds like a lot of fun! Of course, I decided to take a data-driven approach to picking my players, here is my strategy:
- I know how many points per game each player has scored through the season.
- I have a reliable set of win probabilities for each game in the tournament.
The rest is just math to find the expected amount of points I’ll receive for each player.
To get the data for points per game, I wrote a simple scraper of sports-reference.com and grabbed the player statistics for each player in the tournament. Next, I need to find a reliable set of NCAA win probabilities. Considering Nate Silver launched his new fivethirtyeight site with an NCAA blog post, I decided to use his fresh data of win probabilities.
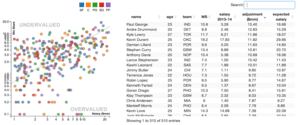
Now that I have the data, the expected value of points for each player can be found by the following formula:
In the above formula, ppg = points per game and wp = win probability.
What I found interesting about my results was that every single player was a very low seed giving me a nice multiplier for each point scored. Another cool finding is that I have four payers from two teams on my squad. Both Tennessee and OK State were favored to win their first game by probabilities of 72% and 52%, respectively.
How did I do so far? One word, domination. Here are the results after the first weekend, I have a very comfortable lead and two players remaining in the game. No one is quite mathematically eliminated, maybe in a near future blog post we’ll simulate the remaining games to give a better representation of how likely I am to win the pool.
Anything more you all would like to see? Leave a comment.