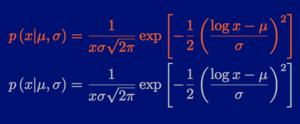Finding the ideal spot in Southeast Michigan
March 14, 2014
With my recent move to the Greater Detroit area, I wanted to increase interest in data science in my new neck of the woods. Since we’ve had success with the growth of the Data Science Chicago Meetup group, I decided to create a similar group for the Southeast Michigan area. In its first month, the group has grown to 50 data enthusiasts. Not bad, considering we’ve yet to have our first meeting!
About that first meeting...since reaching out to the crème de la crème of data scientists in Michigan, one of the recurring questions I’ve been receiving is, “where do you plan to hold the meetup?” Great question. Ideally, the location should be easy to get to for all members of the meetup. Since this is Datascope, we decided to let the data help us find the “ideal” location.
Visualizing the “ideal” locations
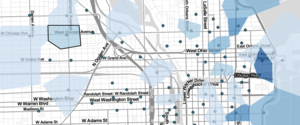
Below, we give you an interactive visual that shows the location of all the Data Science Southeast Michigan meetup members as well as some optimal meetup spots. We also added the option to drag the single location in order to see the average distance traveled for all members to the meetup. You can also view the visualization on a separate page here. Enjoy!
Average distance traveled:
17.0 miles
Drag the green dot around to view average travel distances for all Meetup data scientists.
What does “ideal” mean? Centroid vs. Geometric Median
Our first instinct in finding the right location was to simply find the centroid of all location data points of our members. Although mathematically simple, there are two problems with this approach. Firstly, we actually want to find the point that minimizes the sum of the distance to all other points, not the point that minimizes the sum of the squares of the distances to all other points. From Wikipedia:
“Despite the geometric median's being an easy-to-understand concept, computing it poses a challenge. The centroid or center of mass, defined similarly to the geometric median as minimizing the sum of the squares of the distances to each point, can be found by a simple formula — its coordinates are the averages of the coordinates of the points — but no such formula is known for the geometric median, and it has been shown that no explicit formula, nor an exact algorithm involving only arithmetic operations and kth roots can exist in general.”
Secondly, as Pythagoras showed back in 500 B.C., the Earth is not flat. We need to take into consideration the curvature of the Earth to more accurately calculate distance.
Based on the prior work done by Daniel J. Lewis that uses Weiszfeld’s algorithm to find the geometric median of a set of points, we modified his distance calculation to encompass the spherical shape of the Earth. The code can be found here.
Two locations instead of one
Turns out the geometric median for all of the points is in Southfield, MI. Since I’m running the meetup, I decided to exercise my executive powers and veto that option and explore the data a little further.
When taking a closer look at the data, you can see that the meetup members primarily come from two distinct areas: the Ann Arbor and Detroit suburbs. As opposed to settling on just one location for the meetup, maybe it makes more sense to have two different locations.
Now the problem slightly changes. I want to find two new points that minimize the sum of the distances from all other points to the closest of these two new points. So if each meetup member travels to exactly one of these two new locations, the total distance traveled is minimized. Still with me?
There are many ways to solve this problem (like this and this - we used the latter for our Cheating Commish algorithm). Since we know we want two distinct clusters, a logical choice is K-means clustering, which partitions a set of points into k clusters (2 in our case). Each cluster has a centroid, and so each point in the dataset belongs to the cluster whose centroid is nearest to that point.
After clustering our points and finding the geometric median of each cluster, we found the two locations to be Royal Oak, MI and Ann Arbor, MI. Much more reasonable solutions for a people gathering event!